Reflection from a multi-species material and its transmitted effective wavenumber

Abstract

We formally deduce closed-form expressions for the transmitted effective wavenumber of a material comprising multiple types of inclusions or particles (multi-species), dispersed in a uniform background medium. The expressions, derived here for the first time, are valid for moderate volume fractions and without restriction on the frequency. We show that the multi-species effective wavenumber is not a straightforward extension of expressions for a single species. Comparisons are drawn with state-of-the-art models in acoustics by presenting numerical results for a concrete and a water-oil emulsion in two dimensions. The limit of when one species is much smaller than the other is also discussed and we determine the background felt by the larger species in this limit. Surprisingly, we show that the answer is not the intuitive result predicted by self-consistent multiple scattering theories. The derivation presented here applies to the scalar wave equation with cylindrical or spherical inclusions, with any distribution of sizes, densities, and wave speeds. The reflection coefficient for cylindrical inclusions is also formally derived.

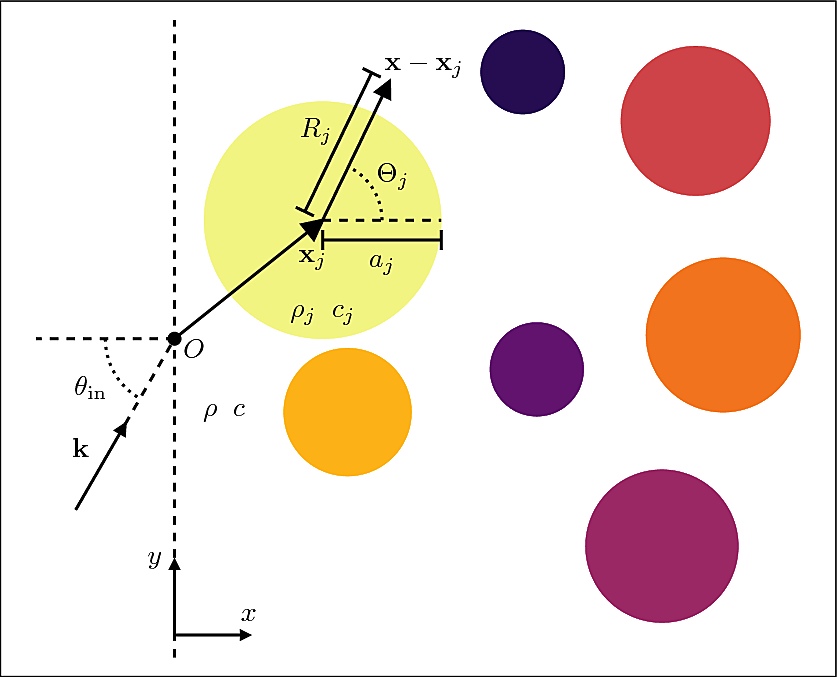
Particulate materials (emulsions, powders, blood) have led to significant advances in foods science and healthcare. To automate the production of these materials or to monitor them in use, waves such as acoustics and light are essential. One open challenge has been to describe waves in particles with different sizes and properties (multi-species). These variations in particle properties are key indicators of performance. This paper is the first to derive a rigorous model, and demonstrates the deficiencies of current ad hoc models.

Quoting the British Standards (ISO 20998-3:2017): “Ultrasonic spectroscopy is widely used to measure particle size distribution (PSD) in colloids, dispersions, and emulsions”. Yet, despite the widespread use and importance of these methods, the ISO publication describes that there does not exist a rigorous model for acoustics in polydisperse particles (multi-species). This paper clearly fills this gap in the knowledge, and provides simply accessible formulas, as well a software package (https://github.com/arturgower/EffectiveWaves.jl) for a vast range of different particle materials.