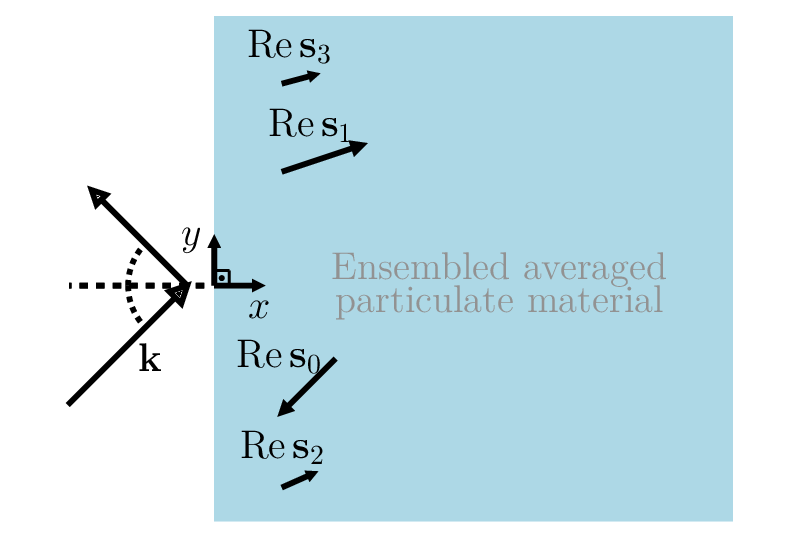
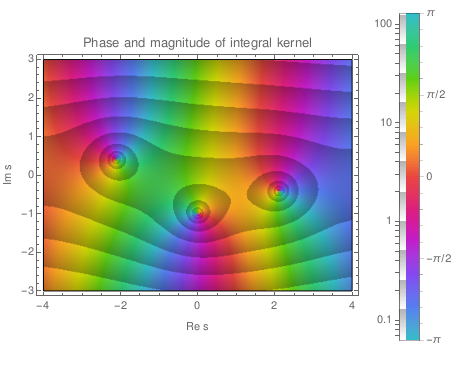
A Proof that Multiple Waves Propagate in Ensemble-Averaged Particulate Materials

Artur L. Gower, I. David Abrahams, William J. Parnell
June 2019
Preprint Code Project Paper Journal

Abstract

Taking into account all the details of an inhomogeneous material is challenging, and sometimes unnecessary. It is often possible to replace the material with an effective medium which is described by only a few macroscopic parameters. To describe wave propagation through a material, the most crucial macroscopic parameter is its effective wavenumber. For this reason, there have been hundreds of studies to calculate this single effective wavenumber. However, here we present a proof that there does not exist a unique effective (complex) wavenumber; instead, there are an infinite number of effective wavenumbers. We also present the exact solution for the reflection coefficient of an inhomogeneous halfspace. For clarity, we present the results for only scalar waves and a two-dimensional material filled with randomly distributed particles or inclusions. We calculate the effective medium by ensemble averaging over all possible inhomogeneities. Though there are many effective wavenumbers, we show through numerical examples that, in most parameter regimes, only a small number of these wavenumbers make a significant contribution to the wave field. The proof is based on the application of the Wiener-Hopf technique and makes no assumption on the wavelength, particle size/type, or volume fraction.

Type
Journal article
Publication
Proceedings of the Royal Society A
Caption: When an incident plane wave $\mathrm e^{i \mathbf k \cdot (x,y)}$ with $\mathbf k = k(\cos \theta, \sin \theta)$, encounters an (ensemble-averaged) particulate material, it excites many transmitted plane waves and one reflected plane wave. The transmitted waves are of the form $\mathrm e^{i \mathbf s_p \cdot (x,y)}$ with wavenumbers $\mathbf s_p = S_p (\cos \theta_p, \sin \theta_p)$ (details in paper) where both $S_p$ and $\theta_p$ are complex numbers. The larger Im $\mathbf s_p$, the more quickly the wave attenuates as it propagates into the half-space and the smaller the drawn vector for that wave above.
These are the kind of complex phase plot you need to deal with to use the Wiener-Hopf method.
multiple scattering wave propagation random media Wiener-Hopf composite materials ensemble averaging

Related