Morphology of residually stressed tubular tissues: Beyond the elastic multiplicative decomposition
Abstract
Many interesting shapes appearing in the biological world are formed by the onset of mechanical instability. In this work we consider how the build-up of residual stress can cause a solid to buckle. In all past studies a fictitious (virtual) stress-free state was required to calculate the residual stress. In contrast, we use a model which is simple and allows the prescription of any residual stress field. We specialize the analysis to an elastic tube subject to a two-dimensional residual stress, and find that incremental wrinkles can appear on its inner or its outer face, depending on the location of the highest value of the residual hoop stress. We further validate the predictions of the incremental theory with finite element simulations, which allow us to go beyond this threshold and predict the shape, number and amplitude of the resulting creases.
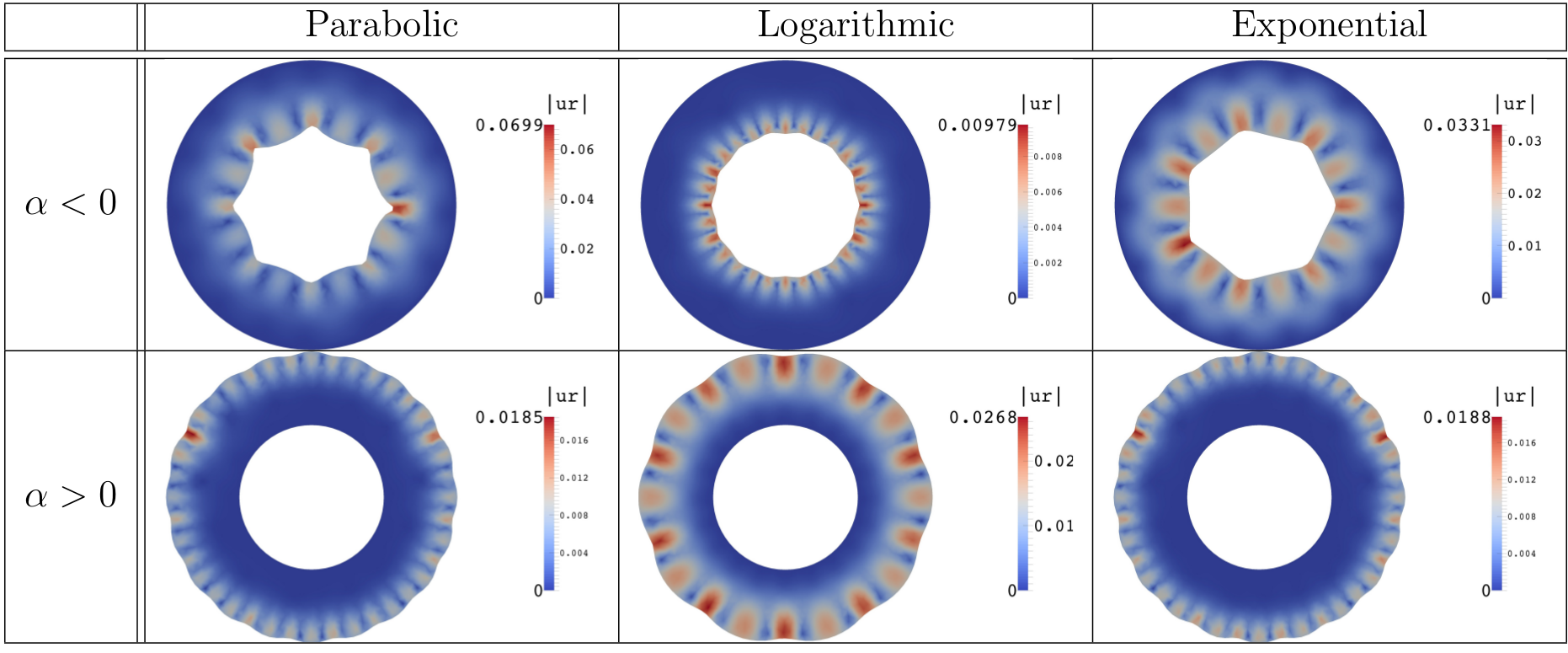
Mammal physiology has an incredible range of patterns, from the folded structure of brains, to the wrinkles along intestines. How do these patterns emerge, and what do they tell us about the mechanics of these tissues? These patterns often result from mechanical instabilities, and previous studies were able to predict a variety of patterns from simple scenarios, such as increasing pressure in a tube. However, these previous studies needed to make use of an abstract construct, a virtual state that the material never occupies. In this paper, we our the first to show that a large variety of tissue patterns can be predicted by simply altering the internal stresses. This clear connection between internal stresses and patterning allows us to clearly connect the tissue’s mechanical function and properties to its pattern.