Elastic & acoustic waves

Our work covers

• Elastic waves, including vibration and ultrasonics
• Constitutive theory of nonlinear elastic materials, which is mostly applied in soft tissue biomechanics
• Coupling soft-tissue stress with instability patterns and elastic waves.

Linear elastic waves

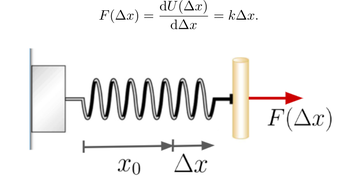
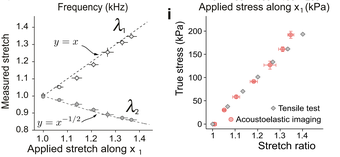
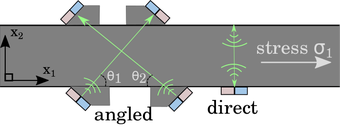
Linear elastic waves cover ultrasonics, and are used to make measurements and assess materials. Work in this includes methods to measure stress through changes in wave-speed with applications in steel and hard solids, medical ultrasound, and measuring extremely thin membranes.

Another theme is use elastic waves in more complex geometries to measure shape changes as well as sources and stress. Our first paper on the theme …

Ultrasonics

Ultrasonics, and elastic waves, are ideal to monitor and measure materials soft and hard. Elastic waves travel through materials without altering their properties, and are sensitive to changes in mechanical properties. The complexity of elastic waves has benefits and drawbacks.

• Benefits: their complexity makes them versatile, allowing them to travel over great distances as a compact signal, or sweep wide areas quickly along surfaces and interfaces.
• Drawbacks: accurate interpretation of ultrasonic waves requires the use of mathematical models, signal processing techniques, and computer codes, which can be time-consuming.

The motivations to work on ultrasonics include:

Non-destructive testing. Ultrasonic methods are commonly used in non-destructive testing (NDT) applications, such as inspecting welds, detecting cracks in materials, and evaluating the integrity of structures. Mathematical models can help us develop new NDT methods that are more accurate, efficient, and reliable, by predicting how ultrasonic waves behave in different materials and under different conditions.

Medical applications. A technique called shear wave elastography uses a standard ultrasound machine (with a high frame-rate) to produce and visualise elastic shear waves propagating in soft tissue. We use mathematical models to understand what these shear waves can tell us, and how best to generate these shear waves.

Below we discuss some examples.

Point impact on a surface

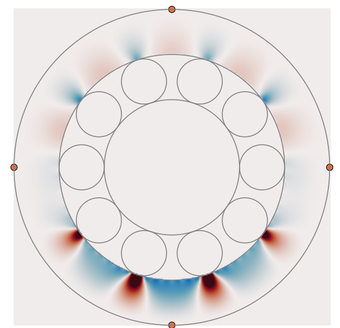
When an anisotropic solid is hit at one point, the solid will react by sending waves out in all directions. Because the solid is anisotropic, these waves travel at different speeds in different directions, which creates unique patterns.

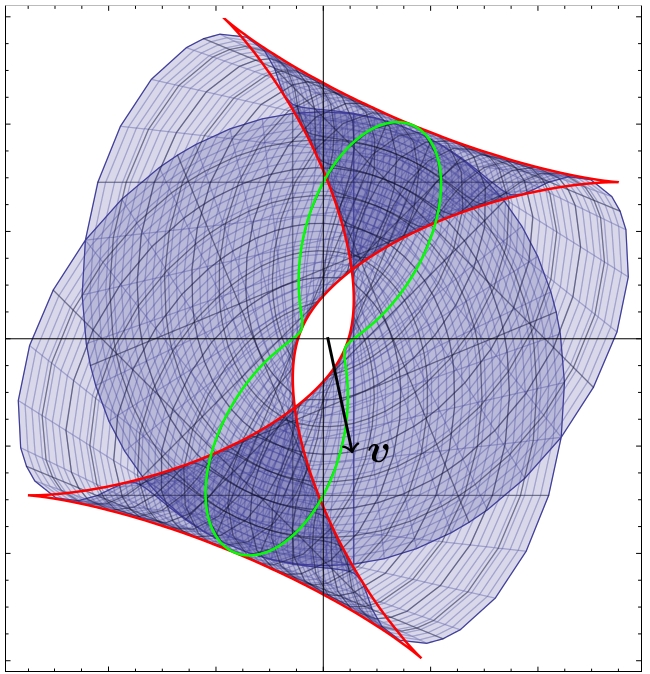
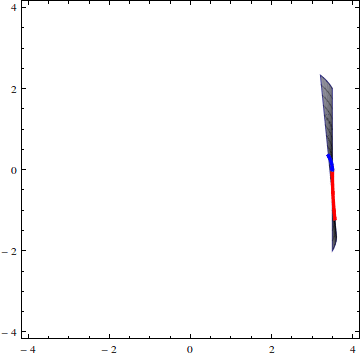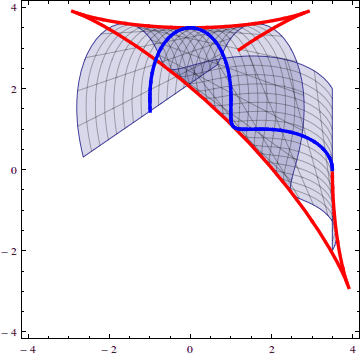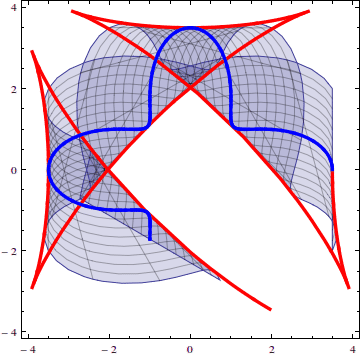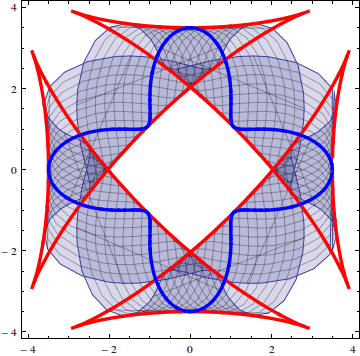
The work I have done on plane surface waves can be used to predict the result of these point impacts, among other applications.