The constitutive relations of initially stressed incompressible Mooney-Rivlin materials

Abstract

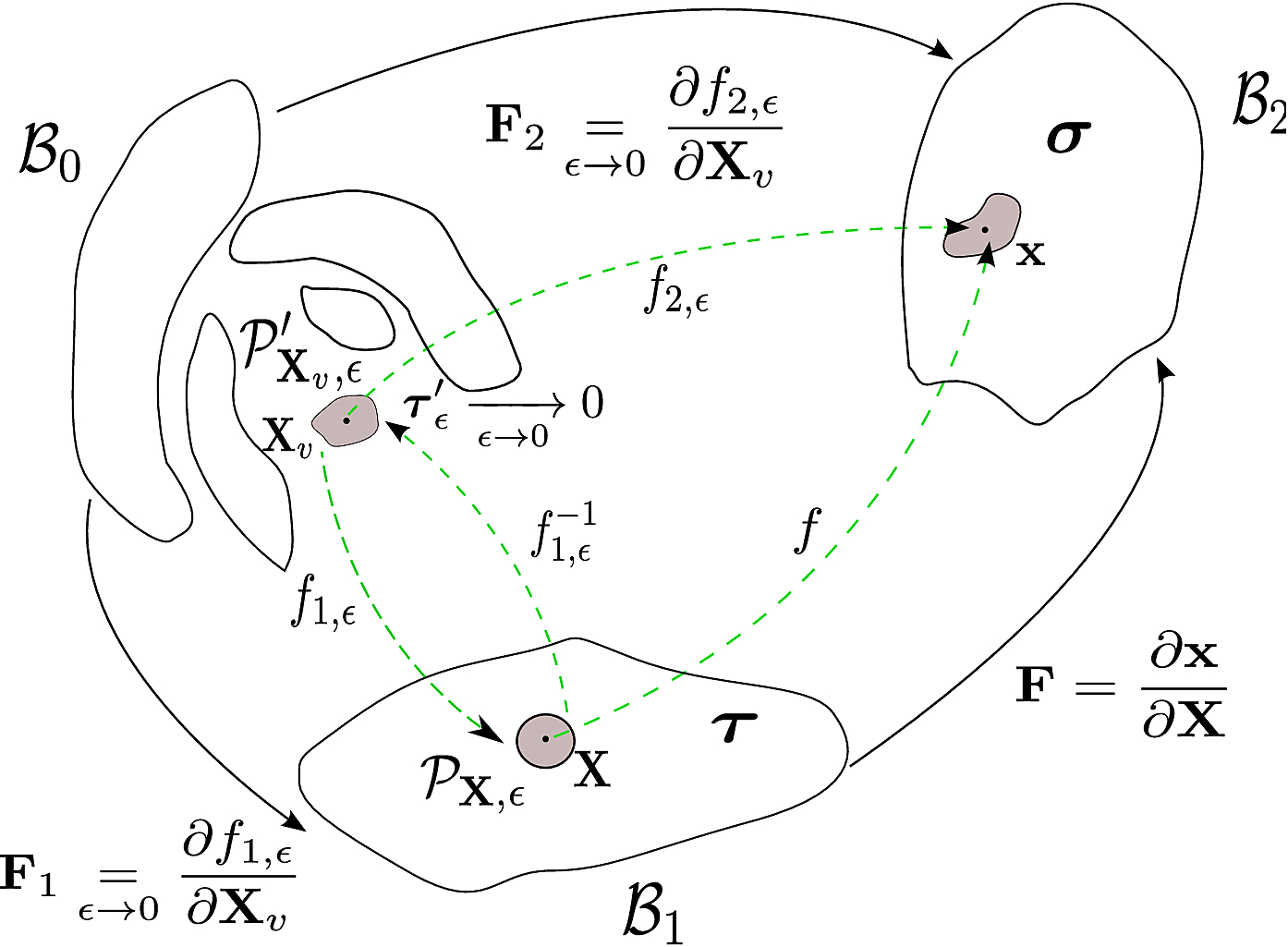
Initial stresses originate in soft materials by the occurrence of misfits in the undeformed microstructure. Since the reference configuration is not stress-free, the effects of initial stresses on the hyperelastic behavior must be constitutively addressed. Notably, the free energy of an initially stressed material may not possess the same symmetry group as the one of the same material deforming from a naturally unstressed configuration. This work assumes that the hyperelastic strain energy density is characterized only by the deformation gradient and the initial stress tensor, using an explicit functional dependence on their independent invariants. In particular, we consider a subclass of constitutive behaviors in which the material constants do not depend on the choice of the reference configuration. Within this theoretical framework, a constitutive equation is derived for an initially stressed body that naturally behaves as an incompressible Mooney-Rivlin material. The strain energy densities for initially stressed neo-Hookean and Mooney materials are derived as special sub-cases. By assuming the existence of a virtual state that is naturally stress-free, the resulting strain energy functions are proved to fulfill the required frame-independence constraints for this special class of constitutive models. In the case of plane strain, great simplifications arise in the expression of the constitutive relations. Finally, the resulting constitutive relations prove useful guidelines for designing non-destructive methods for the quantification of the underlying initial stresses in naturally isotropic materials