Connecting the material parameters of soft fibre-reinforced solids with the formation of surface wrinkles
Abstract
There is a need for more complete models of fibre-reinforced solids that use two anisotropic invariants. However, these models present major challenges. Two of these challenges are how to combine these anisotropic invariants and how to reliably determine the model parameters from experiments. We present an intuitive way to account for both anisotropic invariants through a measure of the fibre extension and a measure of the fibre compression. We suggest that a possible remedy to help characterize a material is to use experiments that cause wrinkles to appear on the surface of the material. We call these wrinkles surface wrinkles. A soft solid will, when compressed, often develop surface wrinkles within its elastic regime, much like when we pinch our skin. Here we use the theory of elasticity to effectively model these large deformations and predict the formation of small superimposed wrinkles. Hence we work through the conditions necessary for the appearance of small surface wrinkles and apply these conditions to a simple model that uses the measures of both fibre extension and compression. It turns out that the angle between the fibres and the surface-wrinkle orientation can be used to distinguish whether the fibres resist only extension, only compression, or a mixture of both. We also uncover a striking tendency of this angle between the fibres and the wrinkle orientation to alternate between only three or four fixed quanta. This trend increases as the fibre strength is increased.
Summary
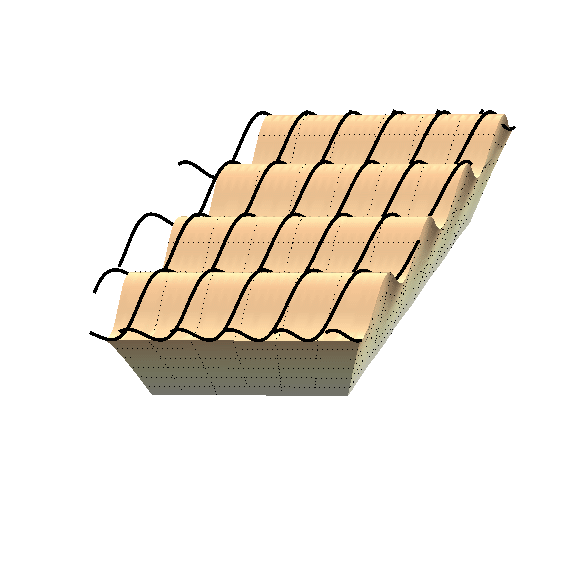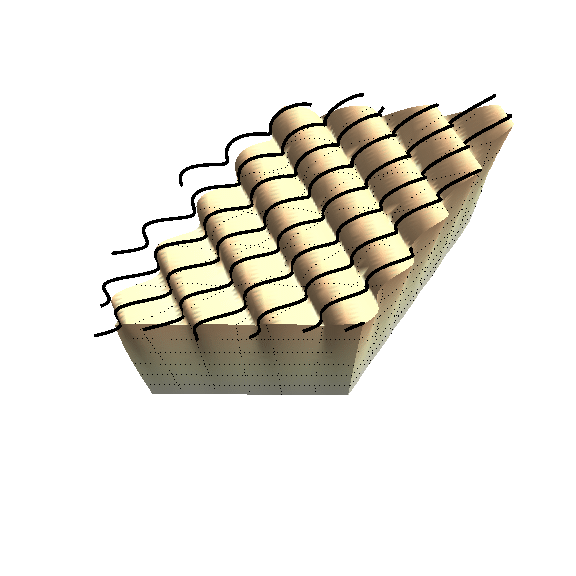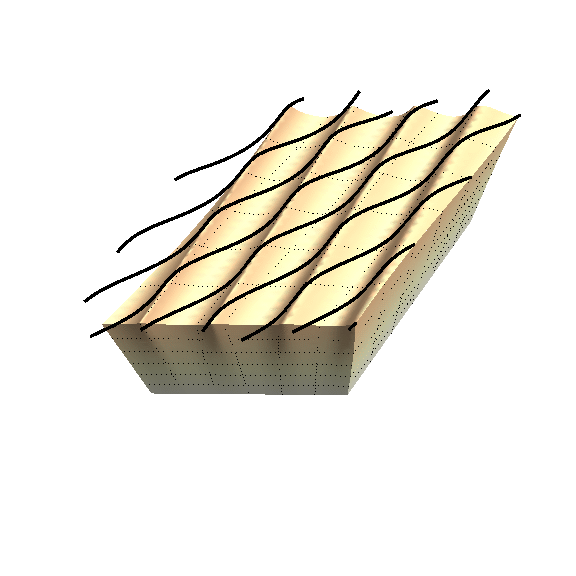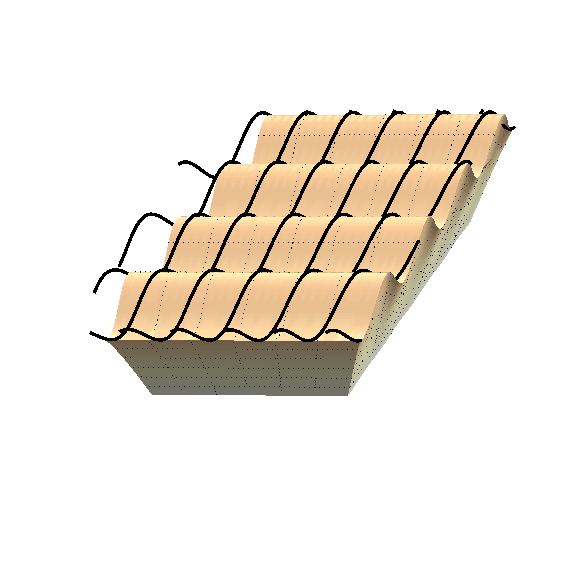
When we compress a soft solid enough, it will form wrinkles on its surface, as shown by the figure below.
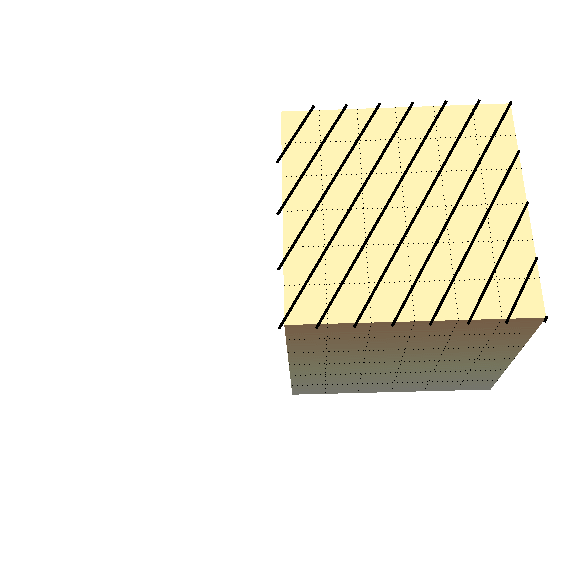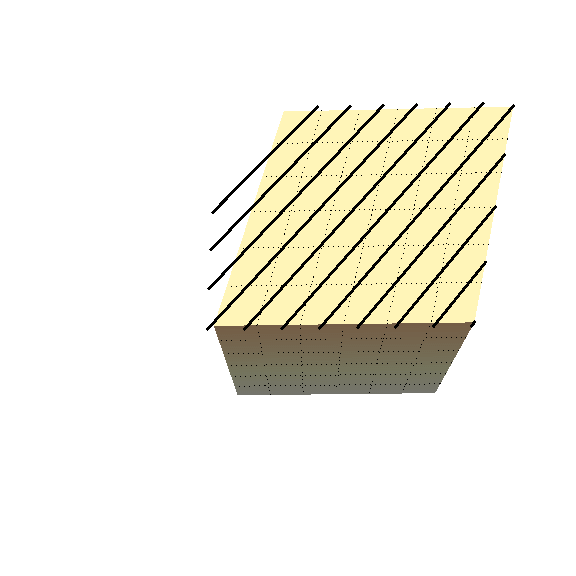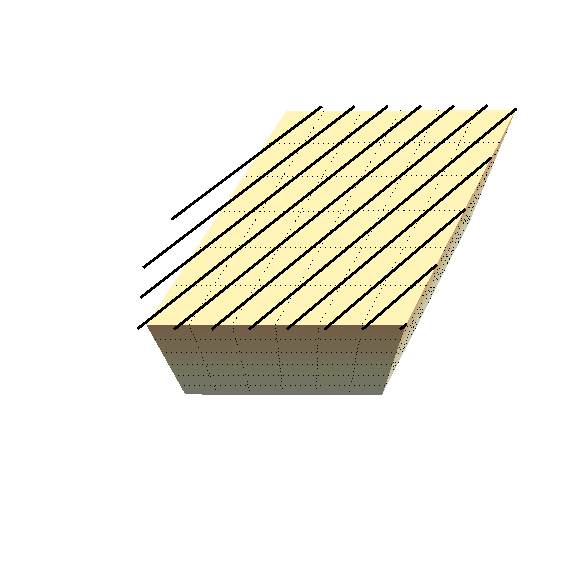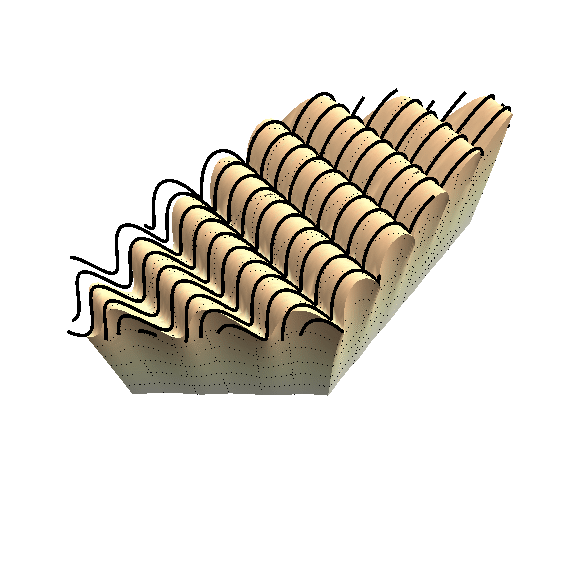
Most biological materials (and industrial) are reinforced with stiff fibres. Knowing how these wrinkles form
- will give us greater control when creating textured surfaces.
- helps us understand how wrinkled surfaces form in biology, like the lining of our gut.
- allow us to use these wrinkles to learn about the material and its fibres.
This last item is the focus of this paper. I study carefully the link between all possible fibres and how they effect the formation of surface wrinkles. The figure below illustrates part of the mathematics.